Існує кілька основних алгоритмів розв’язання задачі сортування масиву. Один з найбільш відомих серед них – сортування вставками. В силу своєї наочності та простоти, але малої ефективності, цей метод використовується в основному при навчанні програмуванню. Він дозволяє розібратися в основних механізмах сортування.
Опис алгоритму
Суть алгоритму сортування вставками полягає в тому, що всередині вихідного масиву формується впорядкований потрібним чином сегмент. Кожен елемент по одному порівнюється з перевіреною частиною і вставляється на належне місце. Таким чином, після перебору всіх елементів вони шикуються в правильному порядку.
Черговість вибору елементів може бути будь-який, вони можуть відбиратися довільно або згідно з алгоритмом. Найчастіше використовується послідовний перебір з початку масиву, де і формується впорядкований сегмент.
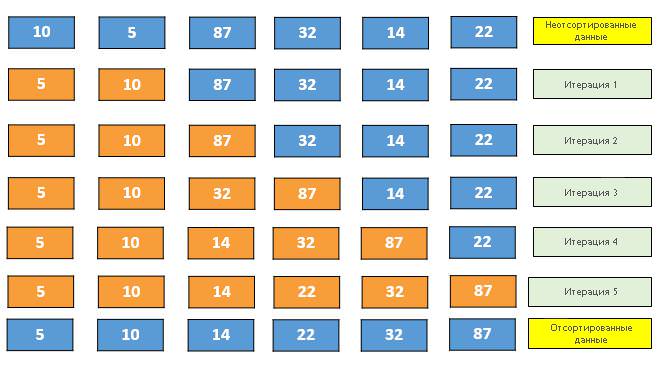
Початок сортування може виглядати наступним чином:
І так далі до кінця початкового масиву.