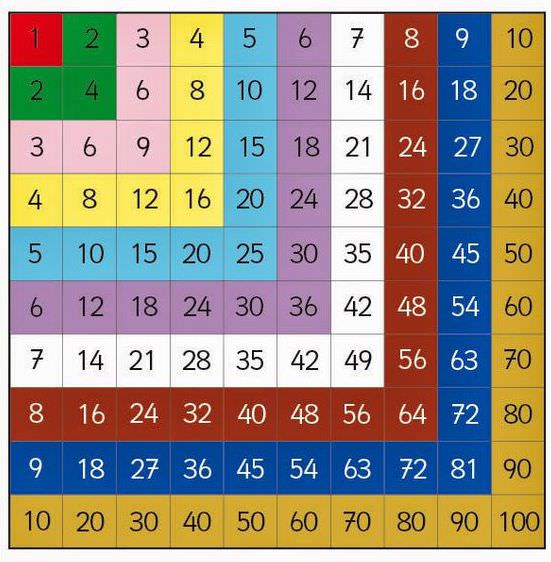
Лінійна функція – це пряма, проведена по поверхні. Вона може поділятися на різні види і моделі. Нижче будуть розглянуті формули її отримання, а також її досягнення досконалості в площині. На малюнках можна буде повністю переконатися в цьому і зрозуміти, як вона повинна виглядати.
Лінійна функція y = kx + b
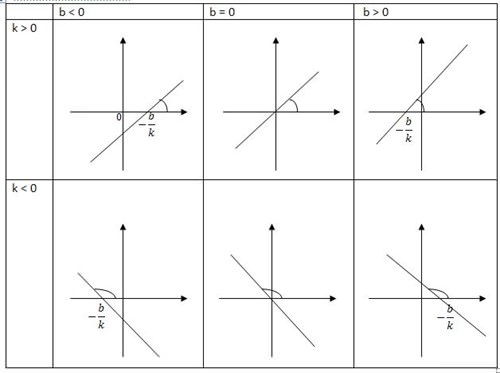
Це значення є точним показником змінної в одному виді. Приріст відноситься до основного властивості лінійної функції, воно стає пропорційним приращенному аргументу. Іншими словами – функція являє узагальнення прямої пропорційності. Пряма – це графік лінійної функції. Від цього і походить її назва. Одна реальна змінна стосується іншої дійсної функції.
Властивості
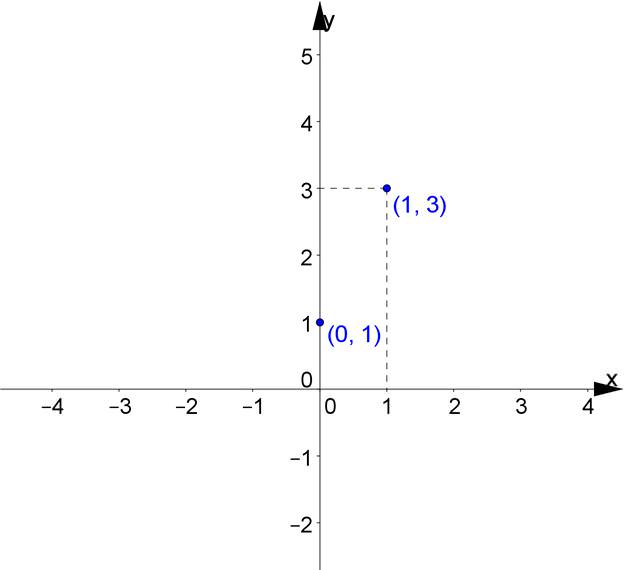
Лінійна функція – це твірна пряма, у якої позитивний напрямок осі абсцис. Одним з її визначають кутових коефіцієнтів є, він визначає тангенс кута а. Пряма, утворена в позитивному напрямку осі абсцис, і є к. Інший координат b вказує координати точок, а також перетин прямої з віссю.
Що являють собою нелінійні функції?
Функції, які не є лінійними, так і називаються – нелінійними. Це математичне співвідношення між змінними. Нелінійні не можна виразити у вигляді y = ax + b. Цей термін використовують у тих моментах, коли необхідно вивчення загального випадку. Починається цей процес з молодших ступенів. При цьому розглядаються квадратичні поправки. Така функція має безперервної кривизною.
Розглянуте нелінійне рівняння – довільне. Прикладом нелінійної функції є у = х2. Часто застосовуються терміни “лінійна функція” з уточненням і додаванням “однорідна”. Вона може бути застосована для точного лінійного відображення Х, що є векторним простором. Лінійна функція – це і є вся система подібних їй.
