Трикутник – одна з основних фігур планіметрії. Саме з нього в шкільній програмі починається вивчення цієї, в якомусь сенсі, геометрії. В залежності від виду кутів цей тип фігур можна розділити на кілька видів. При вирішенні завдань найлегшим зазвичай вважається прямокутний. Для нього існує багато теорем, правил, а також тригонометричні функції, які дозволяють знайти будь-катет або гіпотенузу, знаючи тільки довжину однієї зі сторін і кут (який завгодно за винятком прямого).
Однак якби існував тільки такий вид трикутників, життя учнів середньої і вищої школи була б набагато простіше і безтурботно. Але це не так. Кожна фігура, яку вивчає геометрія, має свої особливості і властивості. Для того, щоб упевнено вирішувати завдання, потрібно знати властивості всіх багатокутників.
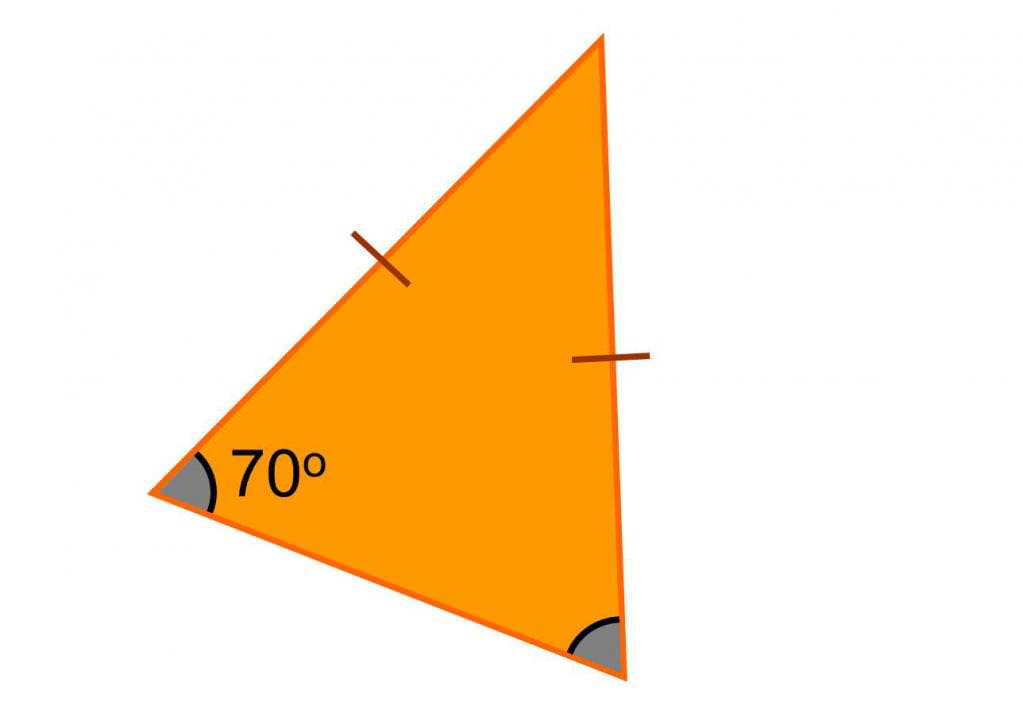
Рівнобедрений трикутник: що це таке і з чим його їдять?
Рівнобедрений трикутник дуже схожий на улюбленця Піфагора, про який говорилося у вступі. Правила, пов’язані з його побудовою або місцем знаходження невідомих елементів, зрозуміє навіть п’ятикласник. Головне – добре орієнтуватися в базових поняттях геометрії та основних елементах плоских фігур.
Властивості рівнобедреного трикутника випливають з його будови. Два кути при підставі такого багатокутника однакові, як і сторони. Відразу з цієї інформації можна зробити певний висновок. Для того, щоб знайти градусну міру вершини, знаючи один з кутів підстави, його потрібно помножити на два і відняти 180°. Дві сторони, крайні точки яких знаходяться у вершині і на підставі, називають бічними.