Відхилення
Щоб зрозуміти, як обчислити дисперсію, треба спочатку розібратися з відхиленням. Його визначення – різниця між значенням, яке приймає випадкова величина та її математичним очікуванням. Грубо кажучи, для того щоб зрозуміти, як величина “розкидається”, потрібно подивитися, яким чином розподіляється її відхилення. Тобто, ми замінюємо значення величини значенням її відхилення від мат. очікування і досліджуємо вже його закон розподілу.
Закон розподілу дискретної, тобто приймає окремі значення випадкової величини записується у вигляді таблиці, де значення величини співвіднесено з ймовірністю її появи. Тоді у законі розподілу відхилення випадкова величина заміниться на його формулу, в якій є величина (зберегла свою ймовірність) та її ж мат. очікування.
Властивості закону розподілу відхилення випадкової величини
У нас записаний закон розподілу відхилення випадкової величини. З нього ми можемо витягти поки тільки таку характеристику, як математичне очікування. Для зручності краще взяти чисельний приклад.
Нехай є закон розподілу якої-небудь випадкової величини: X – значення, p – ймовірність.
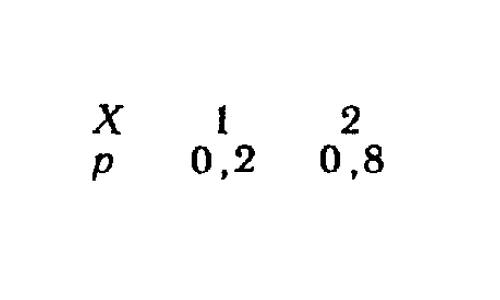
Розраховуємо математичне очікування за формулою і відразу ж відхилення.
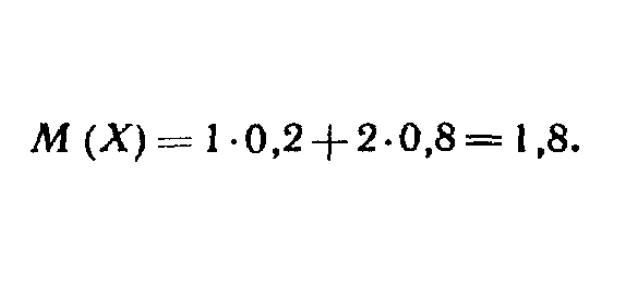
Малюємо нову таблицю розподілу відхилення.
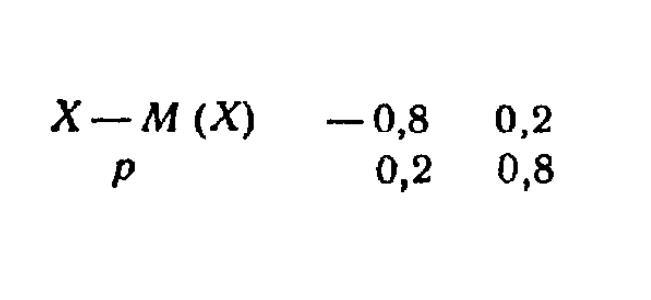
Розраховуємо математичне сподівання і тут.
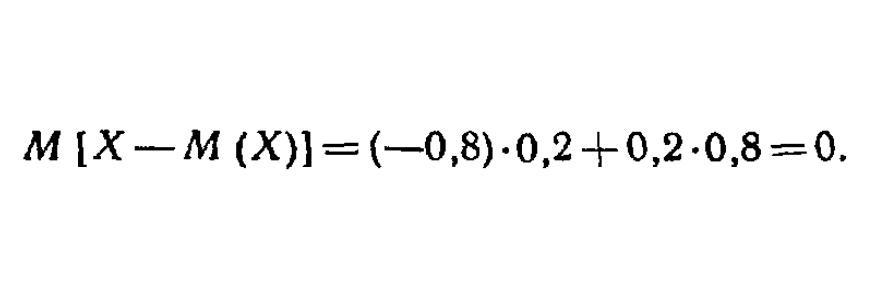
Виходить нуль. Приклад лише один, але так буде завжди: це неважко довести в загальному випадку. Формулу математичного очікування відхилення можна розкласти на різницю математичних очікувань випадкової величини і, як би криво це звучало, математичного очікування мат. очікування (рекурсія, однак), що є одне і те ж, отже, їх різниця дорівнює нулю.
Це очікувано: адже відхилення по знаку бувають як позитивними, так і негативними, отже, в середньому повинні давати нуль.