Поле і сполучення
На завершення дамо два важливі визначення, які надають мало значення для вирішення прикладних задач із комплексними числами, але істотні при подальшому розвитку математичної теорії.
Кажуть, що вирази додавання і множення утворюють поле, якщо задовольняють аксіомам для будь-яких елементів комплексної площини z:
Від зміни місць комплексних доданків комплексна сума не змінюється.
Вірно твердження – в складному вираженні будь-яку суму двох чисел можна замінити на їх значення.
Існує нейтральне значення 0, для якого вірно z + 0 = 0 + z = z.
Для будь-якого z існує протилежність – z, складання з яким дає нуль.
При зміні місць комплексних множників комплексне добуток не змінюється.
Множення двох будь-яких чисел можна замінити на їх значення.
Існує нейтральне значення 1, множення на яке не змінює комплексне число.
Для кожного z ≠ 0, є зворотне значення z-1, множення на яке дає в результаті 1.
Множення суми двох чисел на третє рівносильно операції множення кожного їх них на це число і додавання результатів.
0 ≠ 1.
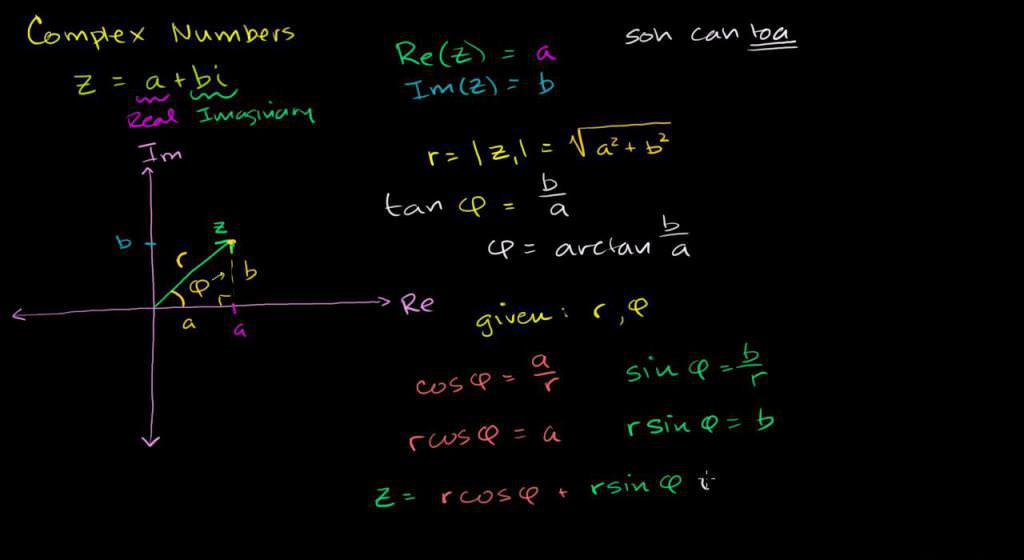
Числа z1 = x + i×y і z 2 = x – i×y називаються спряженими.
Теорема. Для сполучення вірно твердження:
- Пару суми дорівнює сумі спряжених елементів.
- Пару добутку дорівнює добутку сполучень.
- Пару сполучення дорівнює самому числу.
У загальній алгебри такі властивості прийнято називати автоморфизмом поля.
Сторінка: 1 2 3 4 5 6 7 8 9