Рішення на конкретних прикладах
Ось система рівнянь.
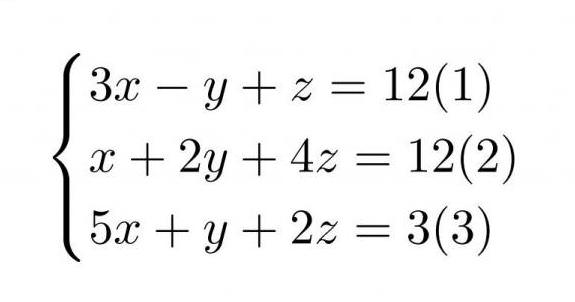
Для зручності краще відразу скласти її матрицю
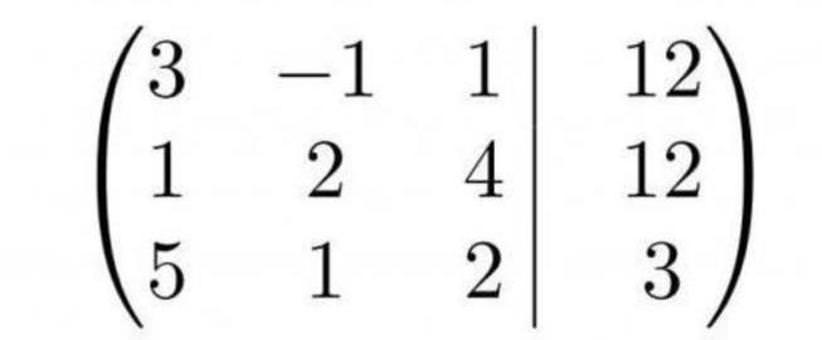
Відомо, що при вирішенні методом Гаусса рівняння, відповідне першому рядку, в кінці перетворень залишиться незмінним. Тому вигідніше буде, якщо лівий верхній елемент матриці буде найменшим – тоді перші елементи інших рядків після операцій звернуться в нуль. Значить, складеної матриці вигідно буде на місце першого рядка поставити другу.
Далі слід так змінити другу і третю рядка, щоб перші елементи стали нулями. Для цього треба скласти їх з першою, помноженої їх на коефіцієнт:
другий рядок: k = (-a21/a11) = (-3/1) = -3
a’21 = a21 + k×a11 = 3 + (-3)×1 = 0
a’22 = a22 + k×a12 = -1 + (-3)×2 = -7
a’23 = a23 + k×a13 = 1 + (-3)×4 = -11
b’2 = b2 + k×b1 = 12 + (-3)×12 = -24
третій рядок: k = (-a31/a11) = (-5/1) = -5
a’31 = a31 + k×a11 = 5 + (-5)×1 = 0
a’32 = a32 + k×a12 = 1 + (-5)×2 = -9
a’33 = a33 + k×a13 = 2 + (-5)×4 = -18
b’3= b3 + k×b1 = 3 + (-5)×12 = -57
Тепер, щоб не заплутатися, необхідно записати матрицю з проміжними результатами перетворень.
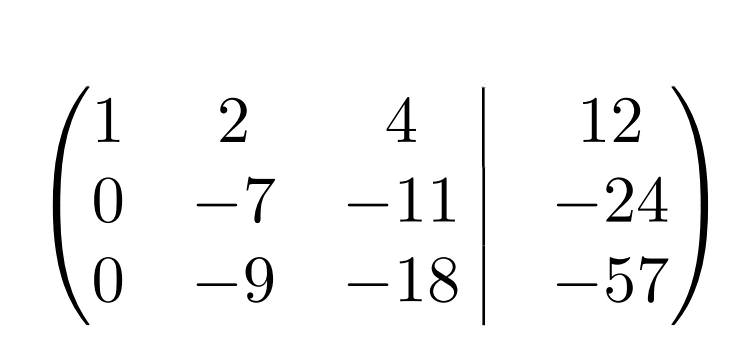
Очевидно, що таку матрицю можна зробити більш зручною для сприйняття з допомогою деяких операцій. Наприклад, із другого рядка можна прибрати всі “мінуси”, множачи кожен елемент на “-1”.
Варто також зауважити, що в третьому рядку всі елементи кратні трьом. Тоді можна скоротити рядок на це число, множачи кожен елемент на “-1/3” (мінус – заодно, щоб прибрати негативні значення).
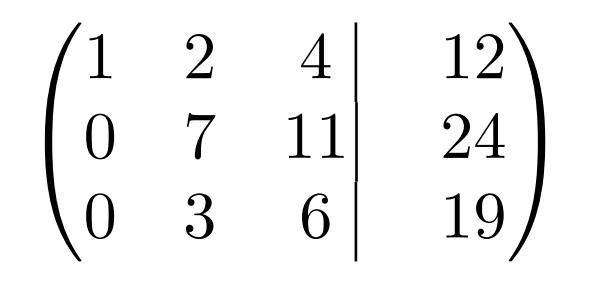
Виглядає набагато приємніше. Тепер треба залишити в спокої перший рядок і попрацювати з другої і третьої. Завдання – додати до третьої рядку другу, помножену на такий коефіцієнт, щоб елемент a32 став дорівнює нулю.
k = (-a32/a22) = (-3/7) = -3/7 (якщо в ході деяких перетворень у відповіді вийшло не ціле число, рекомендується для дотримання точності обчислень залишити його “як є”, у вигляді звичайного дробу, а вже потім, коли отримані відповіді, вирішувати, чи варто округляти і перекладати в іншу форму запису)
a’32 = a32 + k×a22 = 3 + (-3/7)×7 = 3 + (-3) = 0
a’33 = a33 + k×a23 = 6 + (-3/7)×11 = -9/7
b’3 = b3 + k×b2 = 19 + (-3/7)×24 = -61/7
Знову записується матриця з новими значеннями.
| 1 | 2 | 4 | 12 |
| 0 | 7 | 11 | 24 |
| 0 | 0 | -9/7 | -61/7 |
Як видно, отримана матриця вже має ступінчастий вигляд. Тому подальші перетворення системи за методом Гауса не потрібні. Що тут можна зробити, так це прибрати з третього рядка загальний коефіцієнт “-1/7”.
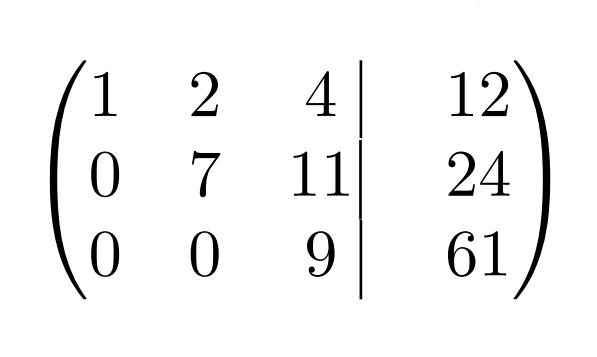
Тепер все красиво. Справа за малим – записати матрицю знову у вигляді системи рівнянь і обчислити корені
x + 2y + 4z = 12 (1)
7y + 11z = 24 (2)
9z = 61 (3)
Той алгоритм, за яким зараз будуть перебувати коріння, називається зворотним ходом методу Гауса. В рівнянні (3) міститься значення z:
z = 61/9
Далі повертаємося до другого рівняння:
y = (24 – 11×(61/9))/7 = -65/9
І перше рівняння дозволяє знайти x:
x = (12 – 4z – 2y)/1 = 12 – 4×(61/9) – 2×(-65/9) = -6/9 = -2/3
Таку систему ми маємо право назвати спільної, та ще і визначеною, тобто має єдине рішення. Відповідь записується в наступній формі:
x1 = -2/3, y = -65/9, z = 61/9.