У даній статті метод розглядається як спосіб розв’язання систем лінійних рівнянь (СЛАР). Метод є аналітичним, тобто дозволяє написати алгоритм розв’язання в загальному вигляді, а потім вже підставляти туди значення з конкретних прикладів. На відміну від матричного методу або формул Крамера, при розв’язанні системи лінійних рівнянь методом Гаусса можна працювати і з тими, що мають нескінченно багато рішень. Або не мають його зовсім.
Що означає розв’язати методом Гаусса?
Для початку необхідно нашу систему рівнянь записати у вигляді матриці. Виглядає це наступним чином. Береться система:
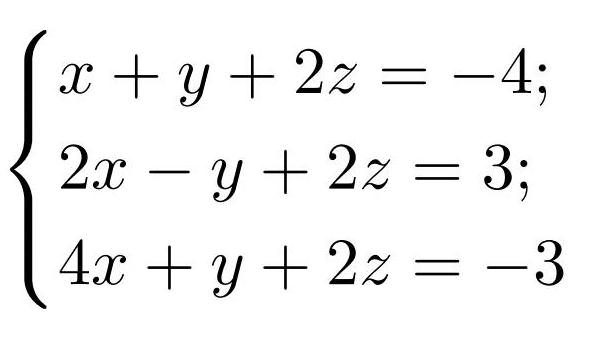
Коефіцієнти записуються у вигляді таблиці, а праворуч окремим стовпчиком – вільні члени. Стовпець з вільними членами відділяється для зручності вертикальною рискою. Матриця, що включає в себе цей стовпець, називається розширеною.
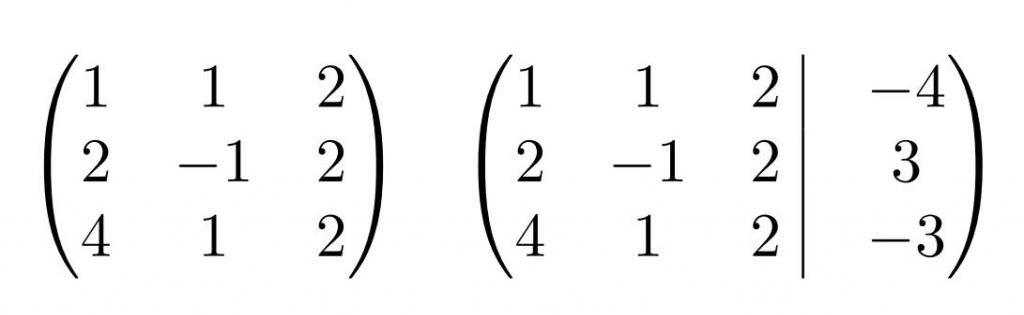
Далі основну матрицю з коефіцієнтами потрібно привести до верхньої трикутної форми. Це основний момент рішення системи методом Гаусса. Простіше кажучи, після певних маніпуляцій матриця повинна виглядати так, щоб у її лівій нижній частині стояли одні нулі:
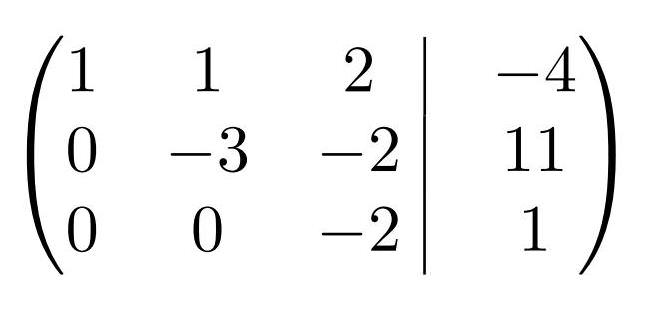
Тоді, якщо записати нову матрицю знову як систему рівнянь, можна помітити, що в останньому рядку вже міститься значення одного з коріння, яке потім підставляється в рівняння вище, знаходиться ще один корінь, і так далі.
Це опис розв’язання методом Гаусса в самих загальних рисах. А що вийде, якщо раптом у системи немає рішення? Або їх нескінченно багато? Щоб відповісти на ці та ще безліч питань, які необхідно розглянути окремо всі елементи, що використовуються при вирішенні методом Гаусса.